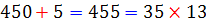بخش پذیری بر 13 و 17 و اعداد مرکب

قانون بخش پذيري بر 13 :

»... اين قانون شبيه بخش پذيري بر 7 است ؛ با اين تفاوت که 13 جايگزين 7 مي شود و به جاي ِ کم کردن ِ 2 برابر رقم حذف شده ، 9 برابر رقم حذف شده را در هر مرحله کم مي کنيم. «...

اين قانون را براي بخش پذيري 6516 بر 13 به کار مي بريم :

با عدد 6516 شروع مي کنيم و رقم يکان آن ، 6 ، را حذف مي کنيم و 9 برابر آن يعني 54 را از عدد باقي مانده کم مي کنيم : 507=54-651. از آن جا که نمي توانيم تشخيص دهيم 507 بر 13 بخش پذير است يا خير ، روند را ادامه مي دهيم .

رقم يکان ِ 507 ، يعني 7 را حذف مي کنيم و 9 برابر 7 را از عدد باقي مانده کم مي کنيم :

13- = 63 - 50

از آن جا که 13- بر 13 بخش پذير است ، عدد اصلي يعني 6516 بر 13 بخش پذير است ؛همچنين عدد 507 نيز بر 13 بخش پذير خواهد بود .

اکنون نشان مي دهيم مضرب ِ 9 از کجا مي آيد . براي اين منظور ، کوچکترين مضرب ِ 9 که رقم يکان ( رقم پاياني ) آن 1 است را جستجو مي کنيم . اين عدد 91 است که رقم دهگان ِ آن ، 9 برابر ِ رقم يکان آن است. در جدول زير ، رقم هاي پاياني ِ ممکن ِ مختلف و تفاضل متناظرشان را ملاحظه مي کنيد :

در هر مورد ، مضربي از 13 يک بار يا بيشتر از عدد اصلي کم شده است . بنابر اين اگر عددي که باقي مي ماند بر 13 بخش پذير باشد ، آنگاه عدد اصلي نيز بر 13 بخش پذير است .

قانون بخش پذيري بر 17 :

»... رقم يکان را حذف کنيد و 5 برابر ِ رقم حذف شده را از عدد باقي مانده کم کنيد ؛ تا زماني که به عدد کوچکي که بتوانيد تشخيص دهيد آيا بر 17 بخش پذير است يا خير ، اين عمل را تکرار کنيد . «...

همان گونه که مشاهده مي کنيد ، اين قانون شبيه بخش پذيري بر 7 و 13 است و نتايج مشابهي براي آن برقرار است .

اميدواريم اين قوانين ، راهنمايي براي شما در جهت به دست آوردن قوانين بخش پذيري بر ديگر اعداد اول باشد .

جهت سامان دادن به بحث خود جدول زير را در اختيار شما قرار مي دهيم . در اين جدول مشاهده مي کنيد که براي بخش پذيري بر هر عدد اول ، چه مضربي از رقم ِ حذف شده را از عدد باقي مانده بايد کسر کنيد :

بسيار جالب خواهد بود اگر شما بخواهيد اين جدول را کامل تر کنيد . اين کار احساس و درک شما را در رياضيات افزايش مي دهد . با آموختن قوانين بخش پذيري بر اعداد اول ، مي توانيم قانون بخش پذيري بر اعداد مرکب ( عددي که اول نباشد ) را دقيق تر بيان کنيم :

قانون بخش پذيري بر اعداد مرکب :

»...عددي بر يک عدد ِ مرکب بخش پذير است که بر تمام ِ مقسوم عليه هاي نسبت به هم اولش بخش پذير باشد. «...

جدول زير به شما در درک قانون بالاکمک مي کند :

ياد آوري مي کنيم که دو عدد نسبت به هم اول ناميده مي شوند هرگاه بزرگترين مقسوم عليه مشترک آنها عدد ِ يک باشد .